<目次>
中学受験生にとっては馴染みのある「つるかめ算」、そもそも何?
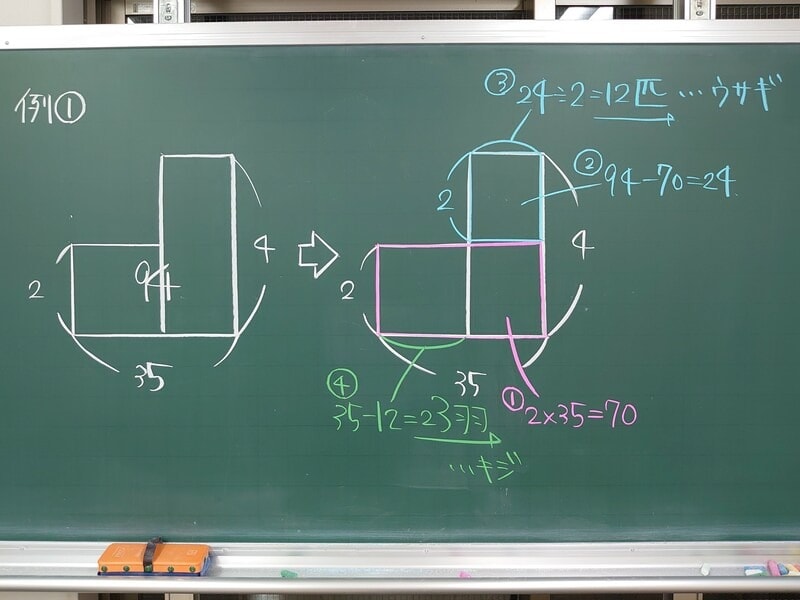
そもそも「つるかめ算」とは何なのでしょうか。中学受験生にとっては馴染みのあるこの言葉、実はもともと古代中国の数学の入門書「孫子算経(そんしさんきょう)」の中で紹介されている次のような問題に由来します。これを中学受験算数で解くと図のようになります。この解法は「面積図」と呼ばれる解き方で、中学受験生にとってはおなじみです。この面積図という解法を使うと、「差集め算」とか「過不足算」といった和と差に関する様々な文章題を解くことができるため、中学受験生にとっては汎用性の高い解法として幅広く学ばれています。例題1 今、キジとウサギが同じカゴの中にいます。頭の数を数えると35あり、足の本数を数えると94本がありました。キジとウサギはそれぞれいくらずついますか。
中学生で習う「連立方程式」を使って解くこともできるため、中学受験塾の中には、方程式を小学生に教えているところもあります。しかし、そうした指導法に対して「小学生に方程式を教えるとは何事だ」という論争が、中学受験業界ではしばしば起こっています。
子ども達が理解できるようになるかどうかは別問題として、私などは「面積図」も「方程式」もどちらも算数の問題を解くための道具に過ぎないのですから、「面積図は認めて方程式は認めない」という主張には、いささか無理があるように感じるのですが、ここでその議論を開始させると、「肯定派」「否定派」が入り乱れて大論争に発展してしまうため、ここではその問題について取り扱うのは避けておくことにします。
本稿では、なぜ中学受験で「つるかめ算」などの問題を扱うようになったのか、その経緯と是非について論じていきたいと思います。
私立中学と塾の“いたちごっこ”により生まれた「特殊算」
つるかめ算や旅人算などの「特殊算」と呼ばれる算数の問題は、なぜ中学入試の問題として採用されたのでしょう。昭和30年頃(1955年頃)の私立武蔵中学の算数の問題を見ると、平面図形や立体図形と呼ばれる問題と並んで差集め算や旅人算と呼ばれる問題も出題されています。いまなら中堅校に出題されるようなレベルの問題が、御三家レベルの古い入試では出題されていたことになります。
しかし当時小学生だった方にお話をお聞きすると、通っていた塾で「差集め算」や「ニュートン算」といったものは習ったことがないとのことでした。
さらに時代が経った私の中学受験の時代(1980年頃)には、すでに「差集め算」や「ニュートン算」を習っていました。しかし現在の中学受験生の算数のテキストにあるような「倍数算」や「年齢算」といった分類はなく、ざっくりと「割合と比の文章題」というかたちで学んでいましたし、「暦算」や「周期算」なども「規則性に関する文章題」というかたちで学んでいました。
いまよりももっと境界線があいまいで、解法も現代のように体系だっていませんでした。

かつて御三家レベルの古い入試で出題されていた問題が、中学受験塾の分析により解法が体系化されていった生まれた特殊算
私立中学側としてはもちろん「暗記力の高い生徒」は欲しいんです。モノが覚えられない生徒は中学の学習で落ちこぼれてしまうわけですから。数学なら因数分解の公式を覚えなければなりませんし、社会なら歴史上の出来事や人物を覚えなければなりません。理科なら元素記号を覚えなければなりませんし、国語なら古典の助動詞を暗記せねばなりません。学習と暗記は切り離して考えることはできないのです。
しかし一方で、「思考力のある生徒」も取りたいわけです。ただの知識の丸暗記だけでは高等数学を解いたり、論述したりすることはできません。
ですから、それぞれの能力を別々にはかる必要があるわけです。役割分担ですね。たとえば社会や理科の暗記単元では主に「暗記力」を、国語では主に「読解力(日本語力)」をはかります。そして算数では「思考力」をはかりたいわけです。
しかしながら塾側の分析により受験算数は丸裸にされ、暗記科目に成り下がりつつあります。そのためいわゆるトップ校と呼ばれる学校では、単純に公式化された「〇〇算」の解法が使えない問題を敢えて出題するようになってきたのです。
公式暗記合戦のような特殊算は「時代遅れ」なのか
ではこうした、「特殊算」と呼ばれる中学受験算数はもはや時代遅れなのでしょうか。確かにそうした側面もあります。いまやトップ校ではほぼ「旅人算」や「倍数算」といった簡単な文章題は出題されなくなりました。しかしこうした学校でも、「旅人算」や「倍数算」の考え方を知らないより知っていた方が、速く解答に到達できるというメリットがあるため、学んでおく必要があるのです。
私立中学側もここが悩みどころで、単に「思考力」だけをはかりたいのであれば、頭の体操のような問題を出せばいいことになります。実際にそのような問題が出題されたこともあります。男子御三家の一角、開成中学では以下のような問題が出題されたことがありました。
しかしこうしたパズル系の問題ですと、いまやネットなどにあふれかえってますので結局「知っているか知らないか」に落とし込まれてしまう恐れがあります。例題2 3・4・7・8の四つの数字を使って四則演算で10をつくりなさい
そのため「ニュートン算と旅人算を組み合わせて解く問題」や「速さとつるかめ算を組み合わせて解く問題」などを出題するようになりました。ところがこうしたタイプの問題も段々と塾のテキストに掲載されるようになってきており(まさに果て無きいたちごっこです)、受験生たちは際限なく演習に時間を費やさなければならなくなってきてしまっています。ネバーエンディングストーリーですね。
結局中学受験を志す子ども達は、つるかめ算や旅人算などの「特殊算」の学習は積んでおく必要があるわけで、「必要悪」みたいなものになりつつあります。
こうした流れを受けて、トップ校以外の私立中学でもそうした問題を一切出題しない学校も増えてきました。また、公立中高一貫校で採用されている「適性検査」式の入試問題を採用する私立中も増加傾向にあります。私立中学側も、算数が「単なる公式暗記合戦」に落とし込まれないよう努力はしているのです。
変わるべきは旧態依然とした大人たち
今の子ども達はいわゆる「デジタルネイティブ世代」と呼ばれます。私たち大人よりもはるかにITC機器を使い慣れています。年号暗記やら漢字やらにしても、いまやネットで簡単に検索できる時代です。そのうちに翻訳機も開発されて英語の学習なども必要なくなるでしょう。そうした子ども達を導くための教育が、依然として「つるかめ算」や「差集め算」などの古い算数でその力をはかろうとするのは、時代錯誤も甚だしいでしょう。つまり今の「デジタルネイティブ世代」に対して、正しく能力をはかることのできる問題を作成できるか、私たち大人の側が試されているといっても過言ではありません。でないと中学受験自体が古き悪しき時代の遺物として、時代の潮流から取り残されてしまいます。
塾と中学校のいたちごっこはいったん休戦とし、公式化できない問題で勝負する入試形態を模索するべきでしょう。たとえば最初の例題1について、以下のような問題はいかがでしょう。
これなら古い「つるかめ算」を、思考力を問う問題に生まれ変わらせることができると思います。私立中学の入試担当の方、是非ご一考いただけたらと思います。
例題3 次の問題は古い中国の書物に出てくる「つるかめ算」という問題です。
今、キジとウサギが同じカゴの中にいます。頭の数を数えると35あり、足の本数を数えると94本ありました。キジとウサギはそれぞれいくらずついますか。
この問題をたけし君は次のように解きました。
94÷2=47
47-35=12……ウサギ
35-12=23……キジ
たけし君はどのような考え方に基づいてこのような解き方をしましたか。説明しなさい。
【関連記事】